Abstract
We present the first-ever moving-mesh general relativistic hydrodynamics solver for static spacetimes as implemented in the code, MANGA. Our implementation builds on the architectures of MANGA and the numerical relativity Python package NRPy+. We review the general algorithm to solve these equations and, in particular, detail the time stepping; Riemann solution across moving faces; conversion between primitive and conservative variables; validation and correction of hydrodynamic variables; and mapping of the metric to a Voronoi moving-mesh grid.
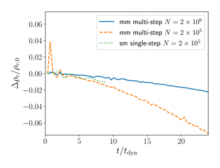
We present test results for the numerical integration of an unmagnetized Tolman-Oppenheimer-Volkoff star for 24 dynamical times. We demonstrate that at a resolution of 106 mesh generating points, the star is stable and its central density drifts downward by 2% over this timescale. At a lower resolution the central density drift increases in a manner consistent with the adopted second order spatial reconstruction scheme. These results agree well with the exact solutions, and we find the error behavior to be similar to Eulerian codes with second-order spatial reconstruction. We also demonstrate that the new code recovers the fundamental mode frequency for the same TOV star but with its initial pressure depleted by 10%