Abstract
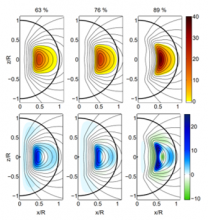
Understanding the properties of the internal magnetic field of neutron stars remains a theoretical challenge. For almost ten years now, twisted-torus geometries have been considered both in Newtonian and general-relativistic equilibrium models, as they represent a potentially good description of neutron star interiors. All of these works have found an apparent intrinsic limitation to geometries that are poloidal-field dominated, with a toroidal-to-poloidal energy ratio inside the star that are ≲10 per cent, unless surface currents are included and magnetic fields are allowed to be discontinuous. This limitation is in stark contrast with the general expectation that much higher toroidal fields should be present in the stellar interior and casts doubt about the stability and hence the realism of these configurations. We here discuss how to overcome this limitation by adopting a new prescription for the azimuthal currents that leads to magnetized equilibria where the toroidal-to-total magnetic field energy ratio can be as high as 90 per cent, thus including geometries that are toroidal-field dominated. Moreover, our results show that for a fixed exterior magnetic field strength, a higher toroidal-field energy implies a much higher total magnetic energy stored in the star, with a potentially strong impact on the expected electromagnetic and gravitational-wave emission from highly magnetized neutron stars.